Erweiterter Dickey-Fuller-Test in Python (mit Beispiel)

Eine Zeitreihe wird als „stationär“ bezeichnet, wenn sie keinen Trend aufweist, über die Zeit eine konstante Varianz aufweist und über die Zeit eine konstante Autokorrelationsstruktur aufweist.

Eine Möglichkeit zu testen, ob eine Zeitreihe stationär ist, besteht darin, einen erweiterten Dickey-Fuller-Test durchzuführen, der die folgenden Null- und Alternativhypothesen verwendet:

H ₀ : Die Zeitreihe ist nicht stationär. Mit anderen Worten, es hat eine gewisse zeitabhängige Struktur und keine konstante Varianz im Laufe der Zeit.

H _A : Die Zeitreihe ist stationär.

Wenn der p-Wert des Tests kleiner als ein bestimmtes Signifikanzniveau ist (z. B. α = 0,05), können wir die Nullhypothese zurückweisen und schlussfolgern, dass die Zeitreihe stationär ist.

Das folgende Schritt-für-Schritt-Beispiel zeigt, wie Sie einen erweiterten Dickey-Fuller-Test in Python für eine bestimmte Zeitreihe durchführen.

Beispiel: Erweiterter Dickey-Fuller-Test in Python

Angenommen, wir haben die folgenden Zeitreihendaten in Python:

data = [3, 4, 4, 5, 6, 7, 6, 6, 7, 8, 9, 12, 10]

Bevor wir einen erweiterten Dickey-Fuller-Test an den Daten durchführen, können wir ein schnelles Diagramm erstellen, um die Daten zu visualisieren:

import matplotlib.pyplot as plt

plt.plot(data)

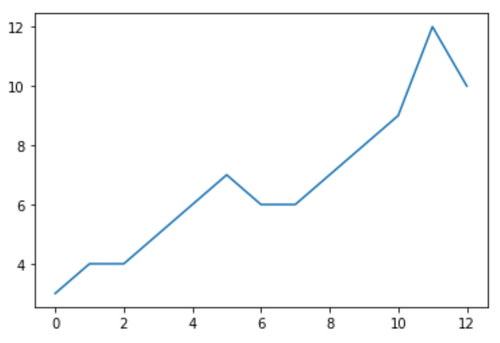
Um einen erweiterten Dickey-Fuller-Test durchzuführen, können wir die Funktion adfuller() aus der statsmodels- Bibliothek verwenden. Zuerst müssen wir statsmodels installieren:

pip install statsmodels

Als Nächstes können wir den folgenden Code verwenden, um den erweiterten Dickey-Fuller-Test durchzuführen:

from statsmodels.tsa.stattools import adfuller

#Führe einen erweiterten Dickey-Fuller-Test durch
adfuller(data)

(-0.9753836234744063,
 0.7621363564361013,
 0,
 12,
 {'1%': -4.137829282407408,
  '5%': -3.1549724074074077,
  '10%': -2.7144769444444443},
 31.2466098872313)

So interpretieren Sie die wichtigsten Werte in der Ausgabe:

• Teststatistik: -0,97538
• P-Wert: 0,7621

Da der p-Wert nicht kleiner als 0,05 ist, lehnen wir die Nullhypothese nicht ab.

Dies bedeutet, dass die Zeitreihe nicht stationär ist. Mit anderen Worten, es hat eine gewisse zeitabhängige Struktur und keine konstante Varianz im Laufe der Zeit.

Zusätzliche Ressourcen

So zeichnen Sie eine Zeitreihe in Matplotlib
So zeichnen Sie mehrere Serien aus einem Pandas DataFrame
So führen Sie einen Mann-Kendall-Trendtest in Python durch