Durchführen einer Polynomregression in Python

Die Regressionsanalyse wird verwendet, um die Beziehung zwischen einer oder mehreren erklärenden Variablen und einer Antwortvariablen zu quantifizieren.

Die häufigste Art der Regressionsanalyse ist die einfache lineare Regression, die verwendet wird, wenn eine Prädiktorvariable und eine Antwortvariable eine lineare Beziehung haben.

Manchmal ist die Beziehung zwischen einer Prädiktorvariablen und einer Antwortvariablen jedoch nichtlinear.

Zum Beispiel kann die wahre Beziehung quadratisch sein:

Oder es kann kubisch sein:

In diesen Fällen ist es sinnvoll, eine Polynomregression zu verwenden, die die nichtlineare Beziehung zwischen den Variablen erklären kann.

In diesem Tutorial wird erklärt, wie Sie in Python eine Polynomregression durchführen.

Beispiel: Polynomregression in Python

Angenommen, wir haben die folgende Prädiktorvariable (x) und Antwortvariable (y) in Python:

x = [2, 3, 4, 5, 6, 7, 7, 8, 9, 11, 12]
y = [18, 16, 15, 17, 20, 23, 25, 28, 31, 30, 29]

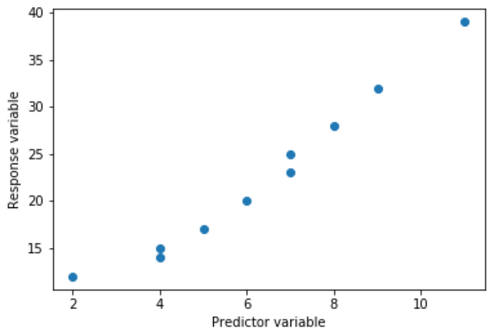
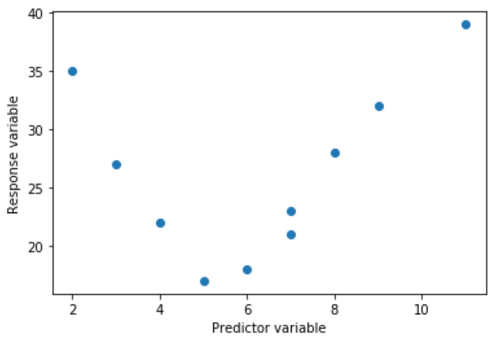
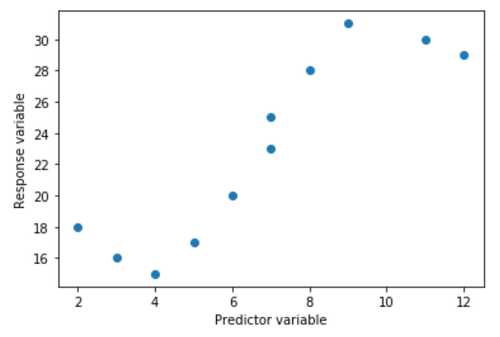
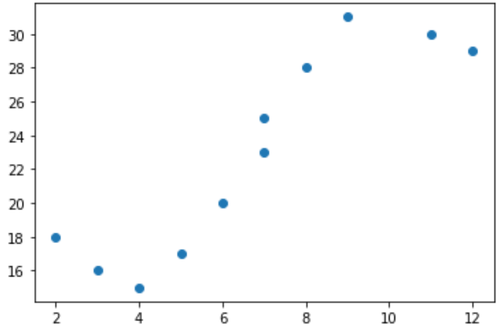
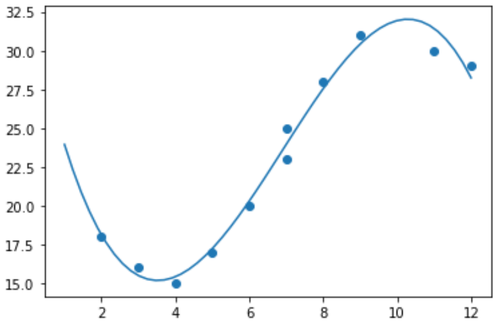
Wenn wir ein einfaches Streudiagramm dieser Daten erstellen, können wir sehen, dass die Beziehung zwischen x und y eindeutig nicht linear ist:

import matplotlib.pyplot as plt

# Streudiagramm erstellen 
plt.scatter(x, y)

Daher wäre es nicht sinnvoll, ein lineares Regressionsmodell an diese Daten anzupassen. Stattdessen können wir versuchen, ein Polynom-Regressionsmodell mit einem Grad von 3 mithilfe der Funktion numpy.polyfit() anzupassen:

import numpy as np

# Polynomanpassung mit Grad = 3
model = np.poly1d(np.polyfit(x, y, 3))

# angepasst Polynomlinie zum Streudiagramm hinzufügen 
polyline = np.linspace(1, 12, 50)
plt.scatter(x, y)
plt.plot(polyline, model(polyline))
plt.show()

Wir können die angepasste Polynomregressionsgleichung erhalten, indem wir die Modellkoeffizienten drucken:

print(model)

poly1d([ -0.10889554,   2.25592957, -11.83877127,  33.62640038])

Die angepasste Polynomregressionsgleichung lautet:

y = -0,109 × ³ + 2,256 × ² - 11,839 × + 33,626

Diese Gleichung kann verwendet werden, um den erwarteten Wert für die Antwortvariable basierend auf einem gegebenen Wert für die erklärende Variable zu finden. Angenommen, x = 4. Der erwartete Wert für die Antwortvariable y wäre:

y = -0,109 (4) ³ + 2,256 (4) ² - 11,839 (4) + 33,626 = 15,39.

Wir können auch eine kurze Funktion schreiben, um das R-Quadrat des Modells zu erhalten, das der Anteil der Varianz in der Antwortvariablen ist, der durch die Prädiktorvariablen erklärt werden kann.

#Definieren der Funktion zur Berechnung des R-Quadrats
def polyfit(x, y, degree):
    results = {}
    coeffs = numpy.polyfit(x, y, degree)
    p = numpy.poly1d(coeffs)
    #calculate r-squared
    yhat = p(x)
    ybar = numpy.sum(y)/len(y)
    ssreg = numpy.sum((yhat-ybar)**2)
    sstot = numpy.sum((y - ybar)**2)
    results['r_squared'] = ssreg / sstot

    return results

#Finden von R-Quadrat des Polynommodells mit Grad = 3
polyfit(x, y, 3)

{'r_squared': 0.9841113454245183}

In diesem Beispiel beträgt das R-Quadrat des Modells 0,9841. Dies bedeutet, dass 98,41% der Variation in der Antwortvariablen durch die Prädiktorvariablen erklärt werden können.